Prologue

This guy must be crazy!
Another esoteric theory of physics that goes nowhere!
This guy thinks he’s God!

A The Theory of Everything, yes, I wrote that title. And maybe yes to other claims too but that is another story, I am serious here. And with this I don’t mean I have the answer to everything. What I claim is that there is an existing theory, that can accumulate and explain in a uniform way all the wisdom and richness of knowledge developed by human kind (mathematics, philosophy, science, psychology, computers, linguistics, art, sport, finance, religion…). This theory is the framework behind logic, the framework behind emotions, the framework behind intelligence.

You will probably think, well if there was such a Thing like a universal Theory of Everything they would probably teach that at schools… Well they do, but at Ph.D. level in some universities. So you probably again think that, I am about to be bullshitting you with some academic nonsense crap? Nope.

I authentically want to share you this precious knowledge and this is coming from an humble and pure intention, a little gift to humanity, a reminder that we achieved this already. So humanity must not be so bad if we achieved that level of consciousness: a theory of everything. This is not so bad as a result. We’re doing usually much worse 99.99999999999999999999…% of the time no?.

So, are you ready? Take a deep breath, go make yourself a coffee if needed, I will need all your attention.

The journey

Of course explaining you the Theory of Everything will not happen in a couple of hours. Sorry for you lazy social media eaters. You probably didn’t make it until here anyway. So to achieve our goal I propose to write a series of chronicles on the Theory of Everything. The rate of the release of the chronicles is unknown and the length also. Writing is not my main job so I will try to find the time to invest in that project and keep it nourished.

These chronicles are about how to apply the Theory of Everything to philosophy, mathematics, science, religion, psychology and potentially unblock human discoveries in these domains by spreading the Theory of Everything The subjects will cover a wide spectrum but the main objective will usually be to introduce the Theory of Everything concepts through examples, concrete examples from our human life. We may also sometimes focus on a specific domain of knowledge to cover it more deeply through a series of chronicles. In any case I will try to keep it short to read but substancial enough to not be completely trivial.

So where do we start? Of course we start with nothing. So this first chronicle is chronicle zero!

Nothing

So we start from Nothing yes, … But didn’t we already ruined the whole concept by saying something about it! Nothing is the ultimate void. Nothing is like Voldemort in Harry Potter. It’s the concept that you cannot pronounce the name. Yet we need to talk about it seriously because (spoiler…) I am gonna give you for free the first rule (its not a rule per se, more a motto) just like that…

Motto 0: From Nothing comes Everything.

$\xymatrix@1{ \mathbb{0} \ar[r]^{!} & ?}$

Well for sure this sentence doesn’t say much if I don’t show you how deep it is. If I tell you right now that even if that sentence has only four simple words that almost every human can understand (in their own language of course), this sentence is not as simple as it seems. In fact, maybe that sentence is one of the most dense sentence I can imagine from an epistemological point of view. So if you were to ask me to tell one last thing before I die I would most probably pick that line…

This is not new stuff… Lao Tseu said in 4th century BC:

The Tao that is definable is not the Tao immutable.
The name that is nameable is not the Name immutable.

Nameless, it is the origin of Heaven and Earth.
Named, it is the beginning of all things.

Nothingness, it is the inner splendor of Being.
Thingness, it is the outer distinctions of beings.

These two, though different in designation, arise from the same source.
This same source is called the luminous Darkness.

Darkness beyond the Dark,
It is the Opening to the myriad kosmic Wonders.

Latest translation from Yasuhiko Genku Kimura

He definitely used more words than me to express it, so his way is much more profound. My way is like the tweet-size version.

Basically Lao Tseu is telling us that he cannot explain us The Way because putting words on it is defining it as something else than its true reality. In other words, trying to explain absolute concepts (like the absolute Emptiness) is a vain endeavour if you’re going to put words on it (intellectualize it). He’s also saying that the origin of the universe is nameless and how the void (non-being) is necessary to contemplate the true essence (the being).

So what we must take as a lesson from these teachings is that absolute concepts created by our human brains can never be proven “true” from the essence of reality and pure logic. So all theories on all subjects are never “The” theory, a final explanation that covers the subject in its entirety.

So he’s basically telling you that you should not continue reading my essays, no? My interpretation of this part is that the Theory of Everything must be a theory capable of expressing the nature of things from a relative point of view per opposition to an absolute point of view.

Relativity

To explain what I mean let’s use pictures. Imagine you are walking on a train track in between the two rails. We could just model this situation by drawing the two rails as two parallel lines in the planes as seen as figure 1 shows.

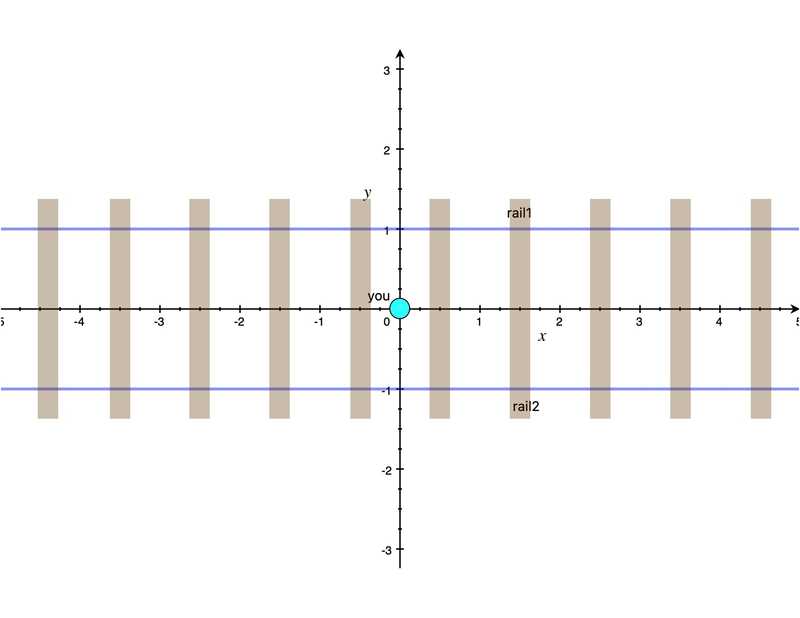
Imagine you are the blue dot in the center. This picture is a representation of the reality using the language of mathematics, the one you learned at high-school yes. In this theory, (euclidean geometry) the two rails are infinite parallel lines. If you remember parallel lines are lines in the plane that never meet (cross). This way of modelling the scene is certainly a useful way to represent it. But it’s definitely not the only way to represent it. Let me show you a different way.

Now imagine what you would see if you were the blue dot and looking right (look in the direction of $x$ axis). You would see something like figure 2.

As is reality the rails look like they meet at a point very very far… On the picture, with the perspective effect, the rails do meet at a point. So from your point of view the laws of geometry are a bit different, in this geometry parallel lines do meet but at a point at infinity ($\infty$). This point in the picture is not like others, it’s distance to our eye is infinite. This other theory of geometry is projective geometry, a theory invented by a french mathematician Jean-Victor Poncelet. Poncelet invented this theory while he was taken as a prisoner by the Russians in the Napoleonic invasion of Russia. Poncelet was walking in the infinite plains of Siberia and had exactly that reflexion looking at the sides of the road. So Poncelet incorporated those special points at infinity inside his theory and started reasoning about them. In this new geometrical universe Poncelet and other mathematicians after him discovered very nice theorems that are not true for the classical euclidean geometry you learned in high-school.

In figure 1 we look at the scene from an absolute point of view, the point of view of God if you want. While in figure 2 we are having a relative point of view. Well which one is right? Both and none at the same time I answer. Both are useful for something, none is the absolute geometry that encompasses all reality inside one theory. So geometry is relative. There is not just one geometry (like we taught you) there are in fact an infinite number of theories of geometry. Euclidean Geometry and Projective Geometry are just two very interesting and studied examples.

So if there are not only one Geometry is there not only one arithmetic, not only one calculus, not only one logic!!! Yes! Exactly! This is exactly the point I am trying to make. We were fooled into thinking that what is taught to us are The Absolute mathematics. This is very wrong…, in fact, I claim that this generalization mistake slowed down human knowledge by a big factor. This is why we don’t actually have a theory of physics that can encompass both the large scale phenomenons (stars, planets, objects,…) and small scale phenomenons (molecules, atoms, photons, quarks, …). This is why we don’t understand totally how our brain functions. Yes this is a BIG mistake to teach geometry as The geometry. Because to really push our human knowledge to the next level we have to also expand our consciousness to view the world in a relative fashion, not as an absolute thing.

This series of essays is about bringing this notion of relativity to the core of the Theory of Everything. The mathematical theory we will use is called category theory. I did a Ph.D. in that domain but I am definitely not an expert of that domain. I had the luck of listening to the lectures of some of the greatest minds behind this very specialized domain of mathematics. Montreal, since the 70’s, has been the world center for the creation of categorical logic and category theory applied to computer science, psychology, linguistics, … I owe this precious gift of knowledge to my dear professor Gonzalo E. Reyes, who had the generosity and patience to accompany me in my laborious transition from absolutism to relativism. Undoing where the educational system brought me was not easy because I was very stubborn.

I decided to write these essays to share this precious gift he gave me with the rest of the world. So I profoundly thank him for this journey inside knowledge and these essays would never have existed if I didn’t had the chance to this great mathematician. Thank you Gonzalo for sharing a bit of your infinite passion.

The beginnings

So let’s start a the beginning. In the Theory of Everything we will draw diagrams to express stuff. Of course these diagrams will need you too to think at an abstract level so it won’t necessarily be easy at first. Please bear with me a bit and the abstraction will be resolved by looking at examples. Understanding the language of the Theory of Everything will definitely need a special intellectual effort. How could a language be able to describe everything human knowledge has constructed and beyond and not be of an abstract nature?

The diagrams we will draw will usually contain basically letters and arrows. We will describe with them some universes of thinking. These universes of thinking are called categories. The letters in those diagrams are called the objects of the category, they are the things of the universe you want to study. The arrows that link objects together are called morphisms, they create relations between the objects. Here is a diagram for a morphism $f$ going from object $A$ to object $B$:

$$\xymatrix@1{ A \ar[r]^{f} & B}$$

A category usually has many of those morphisms. If we had another one from $B$ to $C$ let’s say $g$ then we have the following diagram:

$$\xymatrix@1{ A \ar[r]^{f} & B \ar[r]^{g} & C }$$

In a category, when we have such $f$ and $g$ there must exist another morphism going straight from $A$ to $C$ which is called $g\circ f$ and we draw it like this:

$$\xymatrix@1{ A \ar[r]^{f} \ar@/_/[rr]_{g\circ f} & B \ar[r]^{g} & C }$$

We call that the composition of $f$ followed by $g$ ($g\circ f$) Also, each object $A$ in a category must have an identity morphism $1_A$ that goes from $A$ to itself:

$$\xymatrix@1{ A \ar[r]^{1_A} & A}$$

Then we just have two rules to be respected. The first rule is that when we have $f:A\rightarrow B$ then on each side we have the identity arrows $1_A$ and $1_B$:

$$\xymatrix@1{ A \ar[r]^{1_A} & A \ar[r]^{f} & B \ar[r]^{1_B} & B}$$

and when we compose on either side we get :

$$\xymatrix@1{ A \ar[r]^{1_A} \ar@/_/[rr]_{f\circ 1_A}& A \ar[r]^{f} \ar@/^/[rr]^{1_B\circ f} & B \ar[r]_{1_B} & B}$$

But the rule says that in this case we have $f\circ 1_A=f$ and $1_B\circ f=f$. In other words, composition with an identity morphism does nothing; identity morphisms are neutral for composition in a category.

There is only one last rule in the game for the structure described above to be a category. Suppose we have the following situation:

$$\xymatrix@1{ A \ar[r]^{f} & B \ar[r]^{g} & C \ar[r]^{h} & D}$$

then again we can compose on each side with $g$ to get:

$$\xymatrix@1{ A \ar[r]^{f} \ar@/_/[rr]_{g\circ f} & B \ar[r]^{g} \ar@/^/[rr]^{h\circ g} & C \ar[r]_{h} & D}$$

and finally compose the remaining:

$$\xymatrix@1{ A \ar[r]^{f} \ar@/_/[rr]_{g\circ f} \ar@/_2pc/[rrr]_{h\circ(g\circ f)} \ar@/^2pc/[rrr]^{(h\circ g)\circ f} & B \ar[r]^{g} \ar@/^/[rr]^{h\circ g} & C \ar[r]_{h} & D}$$

then the rule says that $h\circ(g\circ f) = (h\circ g)\circ f$. In simpler terms, it doesn’t matter in which order you compose the morphisms. Let’s summarize this very important definition as Definition 1.

Definition 1: A category $\mathbb{C}$ is composed of objects ($A, B,\ldots$), morphisms ($f:A\rightarrow B$) and a way to $\circ$ to compose chains of morphisms ($g\circ f$) that respects the following rules:
For each object $A$ there is an identity morphism $1_A:A\rightarrow A$.
For any morphism $f:A\rightarrow B$ we must have $f\circ 1_A=1_B\circ f=f$.
For any morphisms $f:A\rightarrow B$, $g:B\rightarrow C$ and $h:C\rightarrow D$ we must have $h\circ(g\circ f)=(h\circ g)\circ f$ (Associativity)

This is very abstract yes but as you will quickly see this structure is all around us and you already know many examples of it. Let’s give some quick examples to clear the fog around this idea.

Example 1: Consider the category $\mathbb{T}$ whose objects are species of known living things ($Dogs$, $Mammals$, …) with the following morphisms. If we take two objects $A,B\in\mathbb{T}$ we will have exactly one morphism from $A$ to $B$ if and only if we can affirm that all $A$’s are $B$‘s. For example, there is exactly one morphism from $Dogs$ to $Mammals$ (because all dogs are mammals). There is also one from $Mammals$ to $Vertebrates$ (since mammals are vertebrates). Composition of these two last morphisms must give a morphism going from $Dogs$ to $Vertebrates$, this morphism also must exist since all $Dogs$ are $Vertebrates$. Identity morphism for each object in $\mathbb{T}$ also clearly exists (since $Dogs$ are $Dogs$, …). And all the rules we enunciated in Definition 1 are satisfied. Take the time to verify them in your head to check if you grasp their meaning here. Let’s draw a small portion of this category $\mathbb{T}$ of taxons. $\xymatrix@1{Dogs \ar@(l,u)[]^{are} \ar[r]^{are} & Mammals \ar@(l,u)[]^{are} \ar[r]^{are} & Vertebrates \ar@(l,u)[]^{are} \ar[r]^{are} & Cordates \ar@(l,u)[]^{are} \\ Cats \ar@(l,u)[]^{are} \ar[ru]^{are} & Alligators \ar@(r,d)[]^{are} \ar[ru]^{are} }$

Example 2: Consider the category $\mathbb{N}$ whose objects are natural numbers ($0, 1, 2, 3, \ldots$) with the following morphisms: there is exactly one morphism between number $n\in\mathbb{N}$ and number $m\in\mathbb{N}$ if and only if $n\leq m$. The shape of this category would look like the following:
$\xymatrix{ 0 \ar@(l,u)[] \ar[r] \ar@/_/[rr] \ar@/_1.5pc/[rrr] & 1 \ar@(l,u)[]\ar[r] \ar@/_/[rr] & 2 \ar@(l,u)[]\ar[r] & 3 \ar@(l,u)[] \ar[r] & \ldots}$
For any $n\in\mathbb{N}$ we have $n\leq n$ so we definitely have an identity arrow for every $n$. Also take some time here to verify that the rules of a category are respected in this example.

Example 3: Consider the category $\mathbb{Set}$ whose objects are sets (as in the theory of sets of Cantor) with the following morphisms: the morphisms between $A\in\mathbb{Set}$ and $B\in\mathbb{Set}$ are simply functions $f:A\rightarrow B$ (a function is a rule that assigns to every $a\in A$ a element $f(a)\in B$. The identity morphism is simply the identity function $1_A$ that sends every $a\in A$ to itself $1_A(a)=a$. Also take some time here to verify that the rules of a category are respected in this example.

We could continue indefinitely to give examples that are very important in human knowledge history. The whole endeavour of this series of essays is about exploring some parts of this huge map defined by the simple and intuitive language of category theory. But bringing you to the level of curiosity and excitement to begin this exploration by yourself is my challenge.

Back to nothing

If you bear with me until here, you have probably won a huge intellectual battle against yourself, against the a priori beliefs of the common sense (mainstream intellectual currents) in which we swim in our modern societies a huge battle over boredom’s maybe! You probably don’t realize yet how far these little steps we made can lead in the understanding of Everything.

I told you one definition and one motto. The motto is not even a rule (from a mathematical or logical point of view) on top of that since it’s formulated in a very sketchy language. Now that I brought you into this weird place you will ask: what do you expect from me? Well, I am asking you to do the one of the most difficult task from an intellectual point of view: to forget about all a priori knowledge about anything: to jump into space $\mathbb{0}$ where there is nothing!

In $\mathbb{0}$ there is no notion of space, time, orientation, causality, … there is no notion of laws of physics, the are no mathematics, no logic! If you get you brain to go into this space then contemplate it as long as you can and come back to me with your clean brain… free of any a priori knowledge and misconceptions about everything. Because with the point of the theory of everything is that you don’t have to (and should not) rely on a priori knowledge and beliefs about the universe, life, knowledge. So you have to forget what you know/believe about space, time, mathematics, logic… Because instead of imposing you some a priori knowledge on these structures we are going to build them from nothing. So if you make your part about going to nothing I can take you somewhere from there.

So please bear with me and come to this non-universe of $\mathbb{0}$ where time, logic, space, things do not exist and cannot even be defined. On this untouchable ground we can construct time but the resulting notion of time will be more general that the one you think is the true nature of time in your a priori knowledge. Because in the The Theory of Everything, time is not given. A universal ambiant abstract time of Newton, or a local observer time of Einstein is not a given thing emerging from the universe as a given incontestable fact. It cannot be… because the Theory of Everything would not explain some experimental results of atomic scales experiments that are simply incompatible with this notion of classical time. So first we have to build a notion of time from nothing that is non-classic in some sense and then we have to verify if this notion can be constructed in our models of the universe and if it stands in with observations of the small and of the large (quantum experiments and classic universe gravitational physics of general relativity).

So forget about all a priori, do you have this blank state of mind, ready? This is the pure meditative state of your brain, this is the state monks are meditating to reach. So $\mathbb{0}$ what about it… Is $\mathbb{0}$ simply the empty category (with no objects and no morphisms), which trivially satisfies the definition above? Would make sense!

Returning to motto 0 now… The motto 0 is simply stating that the category $\mathbb{0}$ has a special property. This property is the following: for any category $\mathbb{C}$ there is a unique functor (we denote it ”$!$“)

$$\xymatrix@1{ \mathbb{0} \ar[r]^{!} & \mathbb{C}}$$

In other words the way to transform nothing into anything must exist and is uniquely determined. We didn’t explain what is a functor yet but for the moment I let you some time to think about this $\mathbb{0}$ and its motto 0. I am kind of tricking you now for keeping it simple.

I feel it’s natural to stop here first the first essay on Theory of Everything. We are in fact at a very interesting point, point $0$. The motto 0 itself is at the boundary between nothing and something, it’s the generative motto certifying that a structure was indeed constructed as a verifiable category in some sense. When we achieve the mental construction of a given category this motto 0 must be valid and it is valid as a tautological truth.

This $\mathbb{0}$ is a category that has a universal property! This property (given by motto 0) says that $\mathbb{0}$ is an initial object category in the category of categories. We will discuss these subjects in detail in further essays but to end the current one with a punch we will state the following amazing fact: $\mathbb{0}$ and it’s motto is how everything is constructed. There is nothing else to know about the rules of the game for understanding the Theory of Everything. The Theory of Everything is using only those principles: the principle of being a category and the principle of $\mathbb{0}$ being a special thing in the sense that it satisfies a (specific) universal property. These ingredients are the DNA of Theory of Everything. Everything else will be constructed from these basic ingredients. Isn’t that amazing? Is life such simple? Yes! But you will see along with the future essays how such simplicity can lead to the best explanation for the universe we live in. Basically how we can construct a very good explanation for time, space, motion, causality, logic, algebra, psychology, philosophy, biology,… using such basic ingredients.